数式は(そんなに)怖くない(3)
本日は,数式怖くないシリーズ3つめの話題です。共分散を取り上げます。
共分散とは
共分散とは2つの変数の変動(または連動)する様子を1つの値に要約したものです。ある変数の値が高くなるときに,他の変数も同じように値が高くなるのか,逆に低くなるのか,それとも連動しないのかを知ることができます。
共分散を求める式
共分散の計算式を眺めてみましょう。
全体として眺めてみると,分数になっていて,1番目からn番目までについて何かを計算したら,すべて足し合わせて,要素数のnで割るという式になっています。要素を全部足して,要素数で割るのは平均ですね。これもなにかの全体的な傾向を真ん中あたりの値で示すという意味がありそうです。
分子を眺めてみると,2つの計算結果の掛け算になっています。カッコの中を見ると,各要素の値から全体の平均が引かれていることがわかります。個々までの計算を表す言葉をまとめれば,割り算,足し算,掛け算,引き算しか出てきていません。つまり,やろうと思えば紙とペンで手計算もできそうです*1。
次に,分子の部分に注目してみます。分子は2つの式の掛け算でできていて,それぞれは,各要素から平均値を引いた値です。ここで大事なのは,この値が正負両方の可能性があることです。要素の値が平均値より大きければ,引き算の結果が正になり,平均値より小さければ引き算の結果は負になります。それで,この結果を掛けているので,考えられるのは次の4つのパターンです。
- 正の値 x 正の値 = 正の値
- 正の値 x 負の値 = 負の値
- 負の値 x 正の値 = 負の値
- 負の値 x 負の値 = 正の値
つまり,両者の正負が一致していれば,掛け算の結果が正,不一致なら掛け算の結果が負になります。共分散は全体として,この傾向を要約したものと考えられるので,全体的に平均からの差の方向性が一致している要素が多いか,差の方向が逆になっている要素が多いかを示していることになります。
最後に,この式は,各要素の値をどんな単位で扱うかによって,共分散自体の大きさが変化してしまうことを指摘しておきます。
グラフから考える共分散の意味
今度は,グラフを使って考えてみます。先程から,平均値を引いた引き算の結果と読んでいるものは,もう少し難しい言葉でいうと偏差と言います。2つの変数の偏差の正負組み合わせをグラフで考えると以下のようになります。このグラフは,各変数の平均値の位置で線が引かれて,4つの領域が作られています。まず,偏差の正負が同じ場合は,グラフ上,データの値が,右上の領域または左下の領域にあることになります。
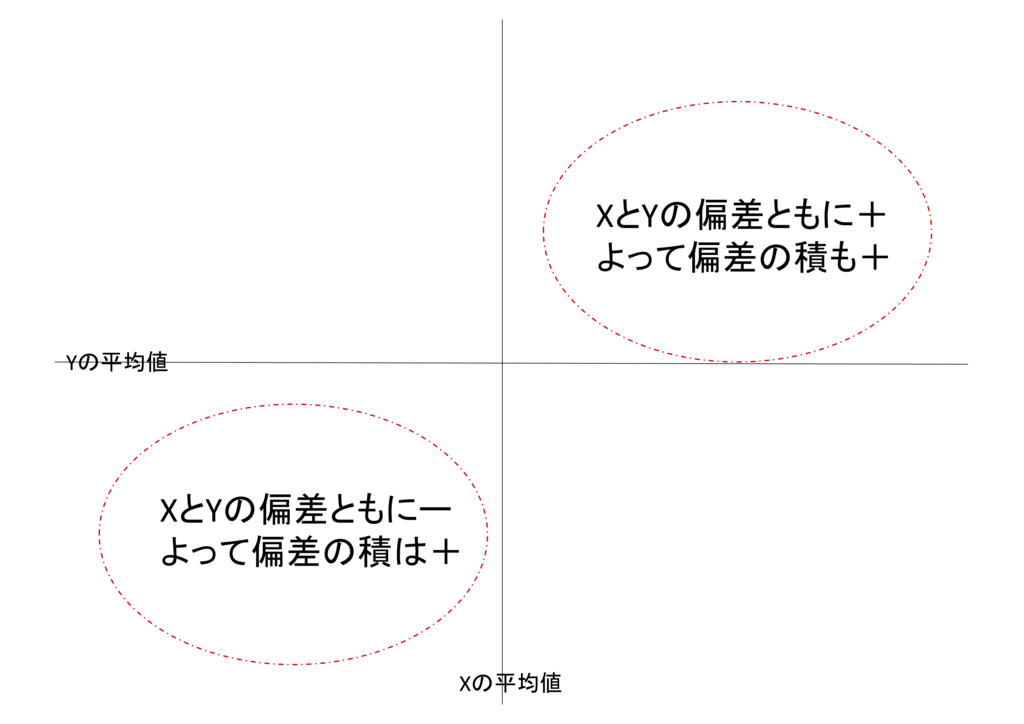

つまり全体的な傾向として,偏差の正負が同じことが多いなら,共分散は正の値になり,グラフ上右肩上がりの傾向を持ちます。逆に,偏差の正負が異なることが多いなら,共分散は負の値になり,グラフ上右肩下がりの傾向を持ちます。このように考えると,共分散を計算することによって,グラフ上でのデータの直線的な傾向の様子を推論することができるようになります。
まとめ
今回は共分散を計算する式を取り上げました。基本的には四則演算しかしていないですし,値の取る意味がわかれば,グラフにデータをプロットするときの様子との対応関係もよく分かると思います。