三平方の定理で理解する回帰分析における分散の分解
今回は、回帰分析の細かいモデルの話を中学校で習う「三平方の定理」を利用して考えてみます。
最小2乗法による推定
回帰分析では、最小2乗法という計算方法で、回帰直線をひくための2つの推定値(切片と傾き)を決めます。何を最小にするかというと実際に観測したデータとモデルによる推定値の間に生まれる誤差(残差と呼びます)を最小にしたいわけです。2乗というのは以下のような計算方法で残差を計算することによります。
- 予測したモデルにおける推定値と観測した値を引き算する。
- 引き算の答えを2乗する。この段階で、推定値が大きくなる場合でも、小さくなる場合でも、2乗した後の値の符号がプラスになります。
- 2乗した値を全て足しあわせます。(これを平方和と呼びます)
この計算過程は分散の計算方法によく似ています。分散では、データの各値の平均からのズレを2乗して全て足し合わせます。さらにこれをデータ数(または自由度)で割ると分散になります。この分散と残差の計算方法の類似を考慮に入れれば、データのばらつきが大きいときは残差(誤差)が大きいといえることが理解できるのではないでしょうか。
平方和の分解と分散説明率
さて、ここで回帰分析における平方和は次のように分解できます。
従属変数の平方和 = 予測された値の平方和 + 残差の平方和
そして分散説明率は以下のように評価されます。
予測された値の平方和 / 従属変数の平方和
つまり、元々ある従属変数のばらつきの何割を予測によってカバーできたかが示されています*1。ここまでの説明は、統計学のテキストで共通に出てくるのですが、わかりそうで分かりにくい表現になっている気がします。
三平方の定理の定理で理解してみよう
三平方の定理は、三角形の斜辺の二乗はその他の2辺のそれぞれの2乗和に等しいというやつです。これが上記の平方和の分解に当てはめられるのですが、それを理解するためには、まず平方和の表現を幾何学的にしてみたいと思います。
このアイデア自体は、自分で思いついたのですが、いろいろ調べてみたところ、類似の説明はすでに以下のサイトや次の書籍で行われています *2。
朝野 煕彦 (2000). 入門 多変量解析の実際 第2版 (KS理工学専門書)
http://d.hatena.ne.jp/rikunora/20131202/p1
従属変数の平方和
まず、従属変数の各サンプルの値から従属変数全体の平均を引きます。以下の図の真ん中から丸までに引かれた線分がそれです。
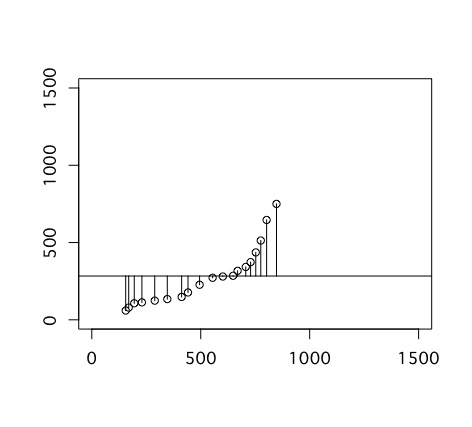
これを2乗するのですが、グラフ内では先ほどの線を一辺とする正方形の面積になります。
これを足し合わせたものが従属変数の平方和です。
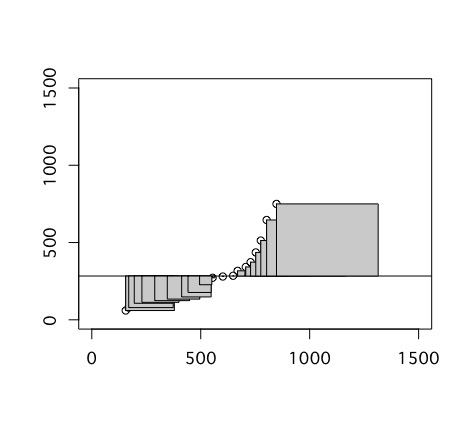
予測された値の平方和
従属変数の平方和と同じような計算方法で、予測された値の平方和を求められます。ただし、今度は、予測された値から従属変数の平均値を引いた線を一辺とする正方形を作り、それを足し合わせます。
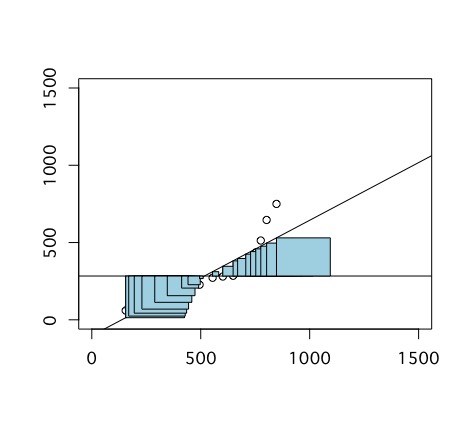
残差の平方和
残差の平方和は、各サンプルの値から、それに対応する予測値を引きます。この線を一辺とする正方形を作り、その面積を足し合わせます。
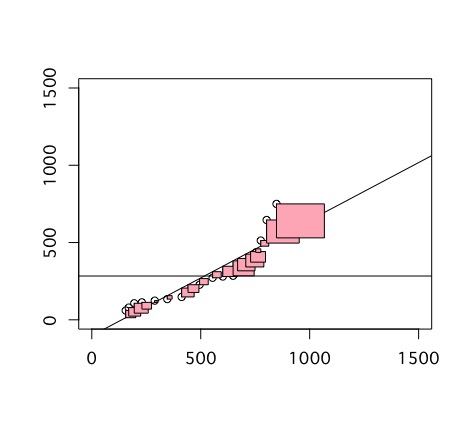
3種類の平方和を三平方の定理に当てはめる
ここまでで3種類の平方和を計算しました。これを三平方の定理に当てはめると斜辺は従属変数の平方和、残りの二辺は、予測された値の平方和と残差の平方和となります。図にすると以下のようになります。
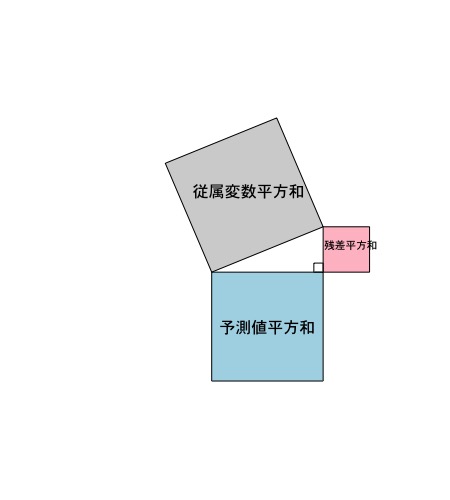
そしてこの図は、以下のような内容の理解に役立ちます。
予測値と残差の相関は0
予測値の平方和と残差の平方和は、直角になるような位置に置かれています。これは、それぞれの値が互いに影響を及ぼさない(つまり相関が0)ことを覚えるのに役立ちます。
従属変数と予測値の指す方向の類似性がモデルの説明率理解に役立つ
予測値の平方和と従属変数の平方和の位置関係は、それに対応する2辺の角度で表せます。そして、この角度は、予測値の平方和が大きくなればなるほど小さくなります。言い換えれば、2辺が指し示す方向がよく似ているということです。これは、予測値の平方和が大きいほど、モデルとしてうまく実データを説明できていることを覚えるのに役立つでしょう。
逆に、モデルとして実データがうまく説明できていないような場合は、予測値の平方和と従属変数の平方和の関係は直角に近くなります。
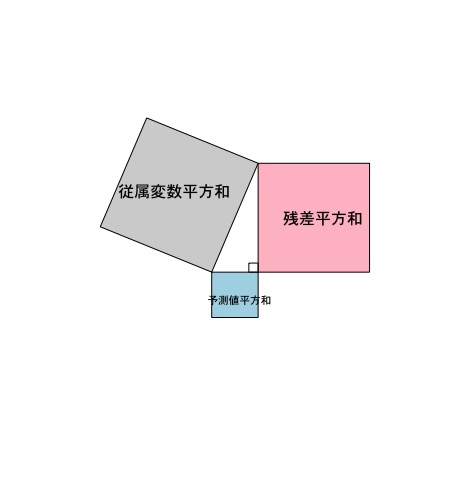
まとめ
今回は、回帰分析の各変数の散らばりを三平方の定理で考えてみました。まとめとして、回帰分析において、従属変数のデータのばらつきは、予測値のデータのばらつきと残差のばらつきに分解できることがわかりました。できるだけ予測値のデータのばらつきを大きくすることを目指して、いろいろな現象を説明、予測してみましょう。
相関と回帰は何が違うか?
今回は、相関分析と回帰分析は何が違うのかを考えます。
相関と回帰の共通点、類似点
相関分析と回帰分析はどちらも、2つの連続量変数(数量型データ)の関係を調べるために行います。ここでの「連続量変数」とは、単に数字で表したデータという意味ではなく、条件が決められています。まず、この変数の尺度水準は間隔尺度です。例えば、1と2の間の1と2と3の間の1は等距離であるということです。また、この変数は確率分布として正規分布を仮定します。
以上のような共通点に加えて、二つの分析によって求めたいことがとても似ています。おおざっぱにいってしまえば、どちらも一方の変数の値の取り方の大小が、他方の値の取り方の大小と結びついているかを調べる分析です。
因果関係の有無が違う
次に、相関分析と回帰分析の違いを考えましょう。決定的に違うのは、因果関係の想定の有無です。相関分析では、変数間の因果関係を想定しません。どちらが原因、または結果でもよくて、相互に影響し合っているのでも構いません。
一方、回帰分析では、想定としての因果を明確にします*1。原因となる側の変数は独立変数、予測変数などと呼ばれます。これに対して結果となる側の変数は、従属変数、応答変数などと呼ばれます。回帰分析は、その予測を式のモデルで表すことができます。
Y = a + bX + e
ここでYは従属変数(つまり予測される側)、Xは独立変数(つまり予測する側)です。aは切片、bは係数または傾き、eは残差と呼ばれています。eを除いた部分は、中学校の一次関数で出てきています。一次関数、つまり、直線を引くための式です。ここで、先ほどの切片と傾きという言葉の意味がわかると思います。切片は横軸の値(独立変数)が0のときの縦軸の値(従属変数)であり、傾きは、直線がどのような角度になるのかを表しています。回帰分析の詳細については、別の投稿でまた書きます。
R言語を利用するときの注意
相関分析では、相関係数を計算します。相関係数は-1から1までの値をとる指標で、-1に近いほど、「一方の変数の値が大きくなるほど、他方の変数の値が小さくなる」ような関係を示しています。この関係のことを負の相関関係と呼びます。また、1に近いほど「一方の変数の値が大きくなるほど、他方の変数の値も大きくなる」関係を示します。こちらは正の相関関係と呼びます。-1と1の中間、つまり0になったときは、2つの変数間に大小関係の結びつきがないことを示しています。このような場合を無相関と呼んだり、2変数が独立の関係であると言ったりします。R言語では、相関係数を求めるためにcor関数を用います。例えばvarAとvarBの相関係数を求めるなら
cor(varA,varB)
と書きます。さらに、この相関係数が0であるという帰無仮説を立てて、相関係数の有意性を検定するにはcor.test関数をつかいます。
cor.test(varA,varB)
ここで引数のとり方を逆にしても同じ値が返されます。どちらが原因とも結果とも決めていないので、強弁する強さのみが示されていると考えられます。
さて、2変数の関係を調べる場合、相関係数のみから結論を導くと誤った結論になることがあります。例えば、変数の中に外れ値と呼べるような極端に大きい値や小さい値が含まれていると、相関係数の絶対値は大きくなってしまいます。なので、相関関係を調べるときには、必ず散布図も書きましょう。散布図を書くにはplot関数をつかいます。
plot(varA,varB)
この例の場合、最初の引数であるvarAが横軸、2番目の引数であるvarBが縦軸の値になります。相関係数の場合と同じで、どちらを先にしても良いのですが、グラフ上のどちらの軸になっているかを覚えておきましょう。これは後で回帰分析のときに大事なポイントになります。
実際に散布図を描いてみると、正の相関が強く見られる場合では、データポイントが右肩上がりになるように分布し、負の相関関係が強く見られる場合では、データポイントの分布が右肩下がりになります。無相関の場合は、全体にまんべんなく分布します。
次に、R言語を利用して回帰分析をするには、lm関数をつかいます。
res <- lm(varB ~ varA) summary(res)
上記の例では、resというオブジェクトに回帰分析の結果を保存しています。これをprint関数の引数として表示すると切片と傾きの推定値しか出力されません。summary関数を使うと、独立変数の傾きの有意性やモデル全体の説明率が表示されます。
また、2つの変数のうちどちらを従属変数に設定するかで、切片や傾きの推定値は異なるので注意が必要です。
相関分析と同じように、回帰分析でも散布図が便利です。以下のようなコードで散布図に回帰直線を加えられます。
plot(varA,varB) abline(lm(varB ~ varA))
ここで重要なのは、回帰分析ではどちらの変数を横軸、縦軸にとってもよかったのですが、回帰分析では、独立変数を横軸、従属変数を縦軸にとらなければならないことです。これを誤ると、回帰直線が散布図上のデータに全く沿わない形で描かれてしまいます。特に、plot関数では最初の引数が横軸になりますが、lm関数の式は従属変数から書き始めるので注意しましょう。
まとめ
以上をまとめると次のようになります。
- 2変数に関して、特に因果関係を想定せずに、共変動する関係にあるかどうかだけを知りたいなら相関分析(cor関数、cor.test関数)
- 2変数に関して、因果関係を想定し、一方が他方に対して持つ影響力の有無や、その予測を知りたい場合は回帰分析(lm関数)
これらを意識しながら、適切な分析方法を選ぶようにしましょう。
*1:想定した因果関係が実在するとは限らないので注意が必要です。むしろそのような因果関係があるかを検証する方法の1つとして回帰分析があります。
アクセス数の合計が200,000を超えました!ありがとうございます!
本日は、ご報告とお礼です。
本ブログのアクセス数の合計が200,000を超えました。前回のご報告でアクセス数100,000突破が今年2016年2月のことでしたので、1年かからずに100,000アクセスをいただいたことになります。
最近のアクセス傾向
これまでのアクセス傾向とそう変わりなく、単純に1日あたりのアクセス数がじわじわと伸びた結果、意外に早い200,000アクセスとなりました。前にもご報告しましたが、このブログは平日のアクセス数が休日のおよそ2倍あります。そして、今年の夏に気がついたのですが、夏休みになってもほとんどアクセス数が減りませんでした。どうやら学生よりも社会人の方にたくさんアクセスしていただいたようです。実務に十分な情報を提供できるよう今後も分かりやすい表現にこだわっていきたいと思います。
データリテラシー向上のためのブートストラップは何か?
今回は、統計や確率、データ解析についてもっと理解し、理解してもらうためのヒントについて考えてみます。最初に言いますが、結論はないです。
確率や統計の学習は難しい
統計やデータは確率という目に見えない概念を論理的、数学的に扱う必要があります。しかも日常的には使わないような論理の展開をすることがあります。例えば、統計学の主な手法の1つに統計的仮説検定があります。これは、言いたいこととは逆の仮定をわざわざ作って、それをさらに否定することで元の主張の正しさを示そうとします。日常生活でそんな面倒なことはしないので、これが自然に身につくというのは考えにくいです。それでも諦めずに使おうと努力しているといつか、使えるようになります。いったん身につければ、それほどの苦労もなく、統計に潜む論理やその実践方法が理解できます。問題はどうやって使いこなせるようになるかです。今回はブートストラップという考え方からこの問題を考えてみましょう。
ブートストラップって何?
ブートストラップというのは、ブーツを履くときに引っ張る紐もしくはつまみです。自分自身で自分を高く上げるという意味で比喩的に用いられます。*1
例えば、ことばの発達ではいろいろなブートストラップ仮説が提案されています。というのも、ことばの学習は
誰もが経験したことでありながら、その学習メカニズムはよくわかっていません。ことばがわからない人にことばで
ことばの使い方を教えても(ややこしいですね)学習は進まないように思えます。でも赤ちゃんは、周りの会話から
単語の意味や文法を見つけていつのまにか使いこなせるようになります。そこで何かしら、自分自身でことばに関する
能力を上げる仕組み、つまりブートストラップがあるのではないかと考えるわけです。例えば、文の抑揚(音の上がり下がりや強弱のリズム)なんかが連続した音声から単語の音の塊を見つけるのに役立つのではないかと言われています。
データリテラシー向上につながるブートストラップ
さて、統計や確率を効率良く理解するためのブートストラップにはどんなものがあるでしょうか。個人的な直感として提案します。
身近な例に頼る?
統計学の教科書にはよく用いられる例があります。二項分布ならコイン投げ(表が出るか裏が出るか)がよく例として用いられます。一様分布ならサイコロを振る例があります。正規分布は、身長や体重がよく使われると思います。これらの例そのものの理解は確かに簡単なのですが、人は日常生活でそんなにコイン投げたりしないし、サイコロも振ったりしないし、周りの人と身長を比べたりもしないですよね。そういう意味ではもっと自分が実際の日常生活にある事例を用いるべきです。例えば、中高生にとって、偏差値70以上を取るのには非常な努力がいるものだし、どんなに怠けていても偏差値30までは下がらないという確かな感覚を持っています。偏差値は、分布として平均50、標準偏差10の正規分布が仮定されています。確率として、偏差値70以上もしくは30以下になるのは全体の5%程度です。正規分布の性質を説明するときには、偏差値を例として挙げることで、「確率的にどれくらいありえないか」ということばの意味をよく理解してもらえると思います*2。
RStudio バージョン1.0でインタラクティブな解析
今回は、R言語を便利に操作するためのアプリケーションRStudioについてです。いよいよバージョン1.0になったRStudioにできた新機能を試してみます。
Rmarkdownファイルを利用した解析(旧バージョン)
RStudioの便利機能の一つにRmarkdownファイルによる解析があります。R言語のデフォルトGUIでは、解析の手順や説明などのテキスト、解析スクリプトとその出力結果、グラフがすべて「別のファイル」として保存されます。あとで結果を見ながらレポートや論文を執筆する際に、スクリプトとその結果をどうにか関連づける必要があります。Rmarkdownファイルを使うとこれをすべて「1つのファイル」で管理し、すべてを1つの HTML、PDFファイルに出力できます。
旧バージョンの問題点
上で書いたようにとても便利な機能を持つRStudioですが、旧バージョンには1つ問題がありました。それは少しでもRmarkdownファイルに変更を加えたらファイル全体を再計算しなければならないことです。小さい解析であれば、再計算の手間はそれほどかからないので、毎回 PDFファイルを作れば良いでしょう。しかし、1回のファイル生成に何分もかかるような大きな解析ファイルでは、1行変更を加えるたびに変更を加えていない箇所まで再計算すると無駄な時間がどんどん増えてしまいます。これを防ぐには、Rの解析コードの結果をチャンク単位で出力できればいいわけです。そのような表示機能は既にjupyterやbeaker notebookなどが実装しています。なので、少し規模の大きな解析になると、そちらのアプリケーションを使わざるを得ませんでした。
RStudioでもインタラクティブな解析が可能になりました
アップデートされたRStudioでは、いよいよインタラクティブな出力表示ができるようになりました。やり方は非常に簡単で、チャンクの右上にある緑の三角ボタンを押すだけ(ショートカットはshift+command+return)です。ボタンを押すと出力結果がチャンクのすぐあとに表示されます。これで、ファイル全体の再計算なしで、必要な箇所のみの改変が簡便に行えます。
Rを使うためのアプリケーション: jupyter vs. RStudio vs. Beaker notebook
Rを便利に使うためのアプリケーションとしてjupyterとRStudioとBeaker notebookが台頭し、アプリケーション間の差がどんどん縮まってきているように感じます。今の所、最終的な結果を PDFファイルとして欲しければRStudio一択だと考えていますが、それも近い将来jupyterやBeaker notebookでエラーのない実装ができるかもしれません。ユーザーとしては便利な機能をしっかり使いこなせるように練習が必要ですね。
「数学ガールの秘密ノート やさしい統計」の感想(2)
今回も「数学ガール秘密ノート やさしい統計」の感想を書きたいと思います。
第4章 「コインを10回投げたとき」
この章では、コインの表が出るか裏がでるかという2つの事象の確率を2項分布で明らかにしていきます。「数学ガール」では、問題への取り組み方にキャラクターによる違いがあって、それが良く見える構成ですね。
「力技」のテトラちゃんは、実際にコインの出方を見ながら「10コインを投げたときの表が出る回数」の期待値を計算していきます。ただし、テトラちゃんも以前よりもいろいろな技が増えてきていて、今回はパスカルの三角形の利用して効率よく確率を計算していますね。「力技」のテトラちゃんに対して、「公式から探索する」「僕」は2項定理による期待値計算を試みます。キャラクターによる取り組み方の違いは、実は第5章まで続いています。「無駄のない教師」のミルカさんは2項分布の期待値の一般化された形式をあっさり導入するからです。統計学の教科書では、最初から一般化された式を紹介する場合が多いと思いますが、こうやって、同じ現象を「力技」「2項定理」「公式」と異なるアプローチで眺めてみると面白いですね。学ぶ側からすれば、手を替え品を替えといった説明からコイン投げという事象を多面的に理解できます。説明の全てを理解できないとしても、どれか一つでも納得できる説明があれば、コイン投げという事象について一定の理解に辿りつけます。
第4章でもう一つ特筆すべきことは、標準偏差を計算していることです。これは、次の章への伏線になっています。それと同時に、期待値(平均値)を計算するだけではデータ解析として不十分で、データのばらつきについてもっと考えようというメッセージになっていると思いました。
第5章 「投げたコインの正体は」
数学ガールシリーズは、最終章のハードルが高いことが特徴的なのですが、本作品の第5章もそれが踏襲されており、なかなか歯ごたえがあります。内容としては前章からの続きでコイン投げで、まず、2項分布が導入されます。ここから2項分布の正規分布による近似へと議論が発展します。さらに、記述統計から推測統計への移行や統計的仮説検定の手続きも紹介されています。高校生の数学という観点からするとするだいぶ背伸びの内容なので、議論をスムーズに展開するうえでミルカさんのリードが大事になりますね。第5章は、ぜひ、じっくりと時間をかけて読むべきです。個人的には、最後に展開されている統計的仮説検定は、別の章として独立させた方がいいかもしれないなと感じました。
この章で特筆すべき内容は、統計的仮説検定でどうデータを解釈するのかの説明です。いわゆるp値を計算するのですが、それを「驚くべきこと」と判断するかどうかとして解釈しています。データについて統計量からp値を計算する過程で、その意味がよくわからなくなる人が多いと思うのですが、「驚くべきこと」という説明方法はわかりやすくて良いなと思いました。
エピローグ
数学資料室での少女と先生の会話です。数学資料室って大学なのでしょうか。内容的には、正規分布の確率密度関数が導入されており、ちらっと二階微分による変曲点の計算まで述べられています。数学科の統計学なら扱う内容だと思いますが、社会科学分野の学科ではここまで扱えませんね。この内容を理解するには、ある程度微分積分の練習を積んでいる必要があります。
全体の感想
数学が好きな高校生、大学1年生に統計学を紹介するならこの本しかないなと思える内容になっていました。あえて続編やスピンオフをリクエストするなら、次の2点を期待したいです。1つは中心極限定理です。推測統計を扱う上では大事な定理の1つなので、ぜひ「僕」やミルカさんによる中心極限定理の議論をぜひ聞いていみたいです。もう1つはシミュレーションによる公式・定理の検証です。数学ガールにはリサちゃんというキャラクターがいます。リサちゃんはコンピュータを使える子で、「乱択アルゴリズム」という作品ではアルゴリズムが丁寧に議論されています。ぜひリサちゃんに登場してもらって、2項分布、正規分布を仮定した乱数生成(ランダムサンプリングの重要性など)やそれを利用した公式、定理の検証を扱ってほしいなと思いました。
「数学ガールの秘密ノート やさしい統計」の感想(1)
今回は、統計学を扱った書籍の感想を2回に分けて述べたいと思います。タイトルでわかる通り、数学ガールの関連書籍で、メインのシリーズというよりは中高生向けのシリーズと認識しています。
そう、著者は結城浩先生です。書評というよりデータリテラシーとのつながりを考えた上での感想です。ガール的な要素のネタバレはしないように心がけますが、各章の概要には触れますので、ご注意ください。
結城先生は統計学をどう扱うのか?
この本を読む前の最大の興味は、結城流の統計学紹介とはどんなものなのかでした。読んでみてわかったのですが、この本は「数学ガール(と僕)からみた統計学の世界」が描かれています。中高生向けのシリーズの1冊として執筆されているのだから当然とも言えますが、このレベル設定が非常に良いと感じました。なぜなら「世間一般の認識」にとても近いと思うからです。もう少し具体的なイメージとしては、「中学、高校は割と理系だったが、大学で統計学関連の科目を取っていない、取らなかった人」です。このような人たちのデータリテラシーを向上させられれば、データがもっと社会で利用されるようになると思います。
第1章 「グラフのトリック」
第1章はグラフで表す便利さとトリッキーさの話です。グラフの作り方ではなく、グラフでどうやって嘘をつくのかに注目しているところがポイントですね。そして、グラフの表面的なメッセージを安易に受け取るのではなく、自分で考える(解釈する)ことが大事なんだと教えてくれています。社会全体のデータリテラシーが向上するには、これがとても大事だと思っているので、このメッセージに非常に共感しました。
第2章 「平らに均す平均」
第2章はいわゆる記述統計量のまとめになっています。平均、中央値、最頻値の3つの代表値に加えて、最大値、最小値、そして分散とデータの特徴を示す指標が一通り扱われています。あとはこれに四分位かパーセンタイルをつけたい気もします。いろいろな用語を出し過ぎて、混乱を招かないようにといった配慮がなされているのかもしれません。あとは、代表値の使い分けについても多少述べられていますね。ここでも、使い分けるためには「何のために代表値を求めるのか」をよく考えようというメッセージを感じます。