統計学の用語のややこしさ(2)
前回に引き続き、今回も統計学の用語で「言い方が違うのに指している内容は同じ」ものを紹介します。
## 回帰分析の原因と結果に関する変数の名前
統計学で利用される分析方法の1つに回帰分析があります。回帰分析では、ある事柄の程度を示す数値を予測するために1つまたは複数の事柄の程度を表す数値を利用し、その予測の程度を検証します。言い換えれば1つもしくは複数の原因となる事柄で結果となる事柄の予測を行います。今回の話題と関連しないので、分析方法の詳細は書きませんが、どんな分野でもよく使われる分析方法の1つです。この「どんな分野でも使われる」というところが実はポイントで、使われる分野によって、以下のように原因と結果を表す変数の呼び名が異なります。
- 原因となる変数の呼び方:独立変数、説明変数、予測変数
- 結果となる変数の呼び方:従属変数、目的変数、応答変数
それぞれ指している内容は同じでも、言い回しが少し違います。本来のどの呼び方をすべきかという議論もあるのですが、ここで大事なのは、呼び名が違っても同じものとして扱えることです。前回同様、複数の本や論文を比較するとには注意したほうが良いでしょう。
統計学の用語のややこしさ(1)
今回は、統計学やデータリテラシーで使われる用語のややこしさについて書いてみたいと思います。
## 統計学の用語
どんな専門領域でもその領域で通じる用語というものがありますよね。細かい言い回しを一言でまとめられれば、話の進みが早くてすみます。ただし、その用語を正しく理解していないと思わぬ誤解が生じてしまう可能性もあります。統計学も専門用語を駆使する領域の一つなのですが、独特のややこしさがあるように感じています。それは「専門用語にもかかわらず、同じ内容を違う表し方をする」ということです。一般に、専門用語は定義が存在するので、違う用語があれば、違い意味・用法で使われるだろうと考えがちですが、統計学やデータリテラシーではほぼ同じ内容を表すのに違う表現になることがあります。
なぜこうなるかというのを考えてみました。原因の一つはおそらく、統計学を利用する人の専門性の違いです。例えば心理学とか生物学とか経済学などの分野では典型的な表現が異なることがあります。そのほかの原因として、研究者による用語の再定義も考えられます。ある理論を提唱する統計学者は同様の内容も違う単語で再定義し、自分の理論内では、一貫してその用語を使っているということがあるように思えます。本人は一貫していたとしても、別の理論で同じ内容が異なる用語で呼ばれているのは混乱の元です。
## 変数の性質を表す用語
同じ内容を異なる表現で表す例として、変数の性質に関する表現があります。変数の性質、例えば、その変数の量は足し算や引き算が可能が不可能かなどです。これは、現象の理解や適切な統計手法の選択に関わる重要な事柄ですが、それを表す用語は様々です。
- 量に関して、足し算や引き算が出来るようなもの: 量的変数、数量データ、間隔尺度データ、連続変数、連続量
- 量に関して、足し算や引き算ができないもしくは無意味なもの:質的変数、質的データ、名義尺度データ、カテゴリー変数、カテゴリーデータ
この二つの区別は、非常に大事なのにもかかわらず、それぞれ表現がいろいろあります。文脈に応じて使い分けることもあるかもしれませんが、ほとんどの場合において、ある表現は、別の表現へと入れ替え可能です。このことを覚えておくと、ある本と別の本では、同じような内容が別の表現を取られているのを見た場合、細かい違いを探さずに、「まあ大体同じ内容のようなので、表現のちがいだけだな」ととりあえずの理解をできます*1。統計学というと数学の一部なのだから、がちがちの定義が並んでいるんだと思いがちですが、初学のうちはあまり悩まずにいろいろな記述を読み進めるというのも大事なように思います。
*1:あとになってから「実はぜんぜん違う意味だった」ということもあるでしょう
大学生への教育を教員による「知的なクローニング」と考えてみる
今回は、大学教育というか教育一般について思うことを書きます。
学生は何を学ぶんだろう?
近年、学生による能動的な学びを促す仕組みが含まれる教授法をアクティブラーニングと呼び、大学をはじめとする高等教育機関で試行錯誤が続いています。学生がぼーっと教授の話を聞くようないわゆる座学が授業だった時代ではもうないようです*1。教員の側も、この状況の変化についていけるように、何をすべきかを考えて、どんどん学ばなければなりません。安定した教授・学習の仕組みが良くも悪くも崩壊した今、改めて教育とは何かを考えるタイミングになったのかなと思っています。
学びの内容を統制できない問題をどうするのか?
アクティブラーニングは、学習者の能動的な学びを促すことに重きが置かれており、ある決められた知識の全てを学ぶことを保証していないように思います。講義で網羅的にコンテンツを取り上げたところで、どうせ全てを学び取れる人はそうそういません。だから、まぁアクティブラーニングになったところで実際に学ばれる内容の幅は変わらないかもしれない。ただ教える側にたってみると「何を学んでいるのかわからない」という状況が不安を呼びます。もしも学生たちがその場その場だけで活動するだけで何にも学んでいなかったらどうしようという気持ちになります。義務教育ではないんだし、何を学ぶか、学ばないかは個人の自由だと思われる方もいるかと思います。しかし、大学には「研究推進」という側面もあり、研究室所属の学生は貴重な共同研究者でもあります。学生に研究を任せられるだけの素養を養ってもらうことが質の高い研究体制の維持の前提となっています。
むしろ教員側がアクティブになったらどうなるか?
そこで、もっと教員がアクティブに指導する体制はどうなのかなと考えてみましょう。学生の自由な発想自体は尊重しますが、研究者である教員自身が研究の動向、難しさ、成功の見込みなどをどのように捉えているのかをオブラートに包むことなく学生に伝えてしまいます。さらに、自分が持っている知識・スキルを学生にオープンにして、教員がやらなくてもいい作業を増やしていく。教えるのに多少の時間はかかりますが、大学院生になれば腰を据えて研究に取り組んでくれる(と期待したい)ので、使った時間以上の進捗を示してくれる(これも期待したい)でしょう。一言でいうなら「知的なクローン」を作るイメージです。
完全なクローンにはならないがそれでよい
学生は、一人の教員だけにつくわけではないですし、自分自身の興味もあるでしょう。なので、完全なクローンにはならないことははっきりしています。しかし、そうであるからこそ、教員が気づかなかったことに気づくかもしれないし、良くも悪くもですが、突然変異的な研究が生まれてきます。
*1:もちろん全ての科目がアクティブラーニングというわけでもありません。また、座学による教授がもっとも効率がよい場合もあります
データの散らばりは誤差にも情報にもなる
今回は、統計を使い始めの人が「ややこしい」と感じそうな話です。
データの散らばりとは
社会科学でも自然科学でも何かデータをとって(難しい言葉使いだと「実証的」)、そのデータから自分の考えを主張したい場合があります。このときデータは、2回以上測ります。なぜかというと、測るたびに値が異なる場合がほとんどだからです。測るたびに値が違う理由にはいろいろあって、「測る条件が毎回微妙に異なる」「測定装置の精度の限界」「実は全く違う条件が混ざっている」などなどです。そして、2回よりももっとたくさん測ることで、データは分布として考えることができます。
データの分布を表す3要素
データの分布は「形」「位置」「散らばり」で特徴付けられます。
「形」
形は全体的な形です。代表的な確率分布である正規分布は左右対称の山形です。サイコロの目の1から6がどの程度の頻度で出現するかというような場合には一様分布が想定されます。
「位置」
位置はその分布が測定に使う指標の中でどこに位置しているかを示します。正規分布だったら、その真ん中の値で代表とします。これは分布の平均値に対応します。
「散らばり」
散らばりは、データの出方が毎回どの程度異なるかを示します。分散や標準偏差といった指標が使われます。これらの指標が大きいほど、平均値からずれの大きいデータがたくさんあることを示しています。
散らばりは誤差です
上の説明にあるように、分散や標準偏差が大きい場合は、平均値からのずれが大きいことを示しています。例えば、ある測定条件やあるグループについて、1つの数でその性質を説明する場合に平均値を使うことが良くあります。しかし、実際には、全員が平均値と同じ値をとっているわけではありません。それでも、その条件やグループの測定を全て同じとみなして、1つの点で表現しています。これを逆に考えれば、散らばりの大きさはその1つの点の確からしさに影響していて、散らばりが大きいほど、1点で表現するのに無理があるようにも見えます。つまり、散らばりの大きさが誤差の大きさに対応しています。
散らばりは情報にもなります
上で述べてきたように、分散や標準偏差は平均値からのずれの指標です。これらの値が大きいほど、一つ一つの値の異なりが大きいとも考えられます。値の異なりが大きければ、それらを簡単に区別できます。こんな風に考えると、散らばりが大きい方が、一つ一つの個体の違いが良く分かると言えます。個体の違いを表すものは個体の情報なので、散らばりそのものが情報の量に対応しているというわけです。例えば、入学試験での合否の判定や順位付けなどではこの考え方が活きてくるので、ばらつきが大きい試験の方が、受験者の能力を判定する上でよいテストとなります。
まとめ:味方によって誤差にも情報にもなる
以上でみてきたように、個体ごとのデータの散らばりはときには誤差として、小さいほどよいものとなります。その一方で、データの散らばりを情報とする見方も可能で、この場合は大きいほどよいものとなります。いずれにしても散らばりの程度を適切に評価していくことが重要です。
2要因の分散分析での交互作用効果と単純主効果検定の関係
今回は、2要因の分散分析をするときの交互作用と単純主効果について説明します。ややこしい話題ですが、具体的なストーリーで説明して、ちょっとでもわかりやすくと思っています。
想定例:学生の専門分野による文章内の図表の挿入効果の違い
今回は、ある文章を読んだ後の理解成績を興味の対象(つまり従属変数)にします。このとき、文系学生(20人)と理系学生(20人)に参加してもらい、文系理系という専門分野の違いが理解成績に影響するかを調べます。
また、文章に関して、図表の有無が操作されていました。これについて図表の有無が理解成績に影響するかを調べます。というわけで、今回は専門分野(理系、文系)と図表(あり、なし)という2つの要因を設定し、従属変数である理解成績に及ぼす影響を2要因分散分析で検討します *1。なお、それぞれの要因の組み合わせの参加人数はそれぞれ10人とします。
主効果
先ずは普通の主効果を考えましょう。図表の有無で理解成績が異なるかを調べます。主効果を検討する場合は、図表の有無のみを考え、学生の専門分野は無視します。つまり、図表ありの文章を読んだ20人の学生と図表なしの文章を読んだ20人の成績を比較します。平均成績を求めたところ、図表なしは平均80点、図表ありは平均85点でした。同じ方式で、専門分野による理解成績の違いの主効果も検討できます。

交互作用
次に交互作用について考えみましょう。交互作用は組み合わせ次第で生じる効果の大きさの違いに注目します。今回の例では、図表の有無による違いの大きさに着眼します。組み合わせによる効果は、図表の有無による理解成績の違いの大きさが文系学生と理系学生とで異なるかを意味します。
以下では、交互作用の出現パターンに関して3つのストーリーを考えてみます。
交互作用なしの場合
最初に交互作用が全くない場合を考えます。このとき、図表の有無による違いの大きさが、文系学生と理系学生で全く同じであるということになります。ちょっとややこしいのですが、違いの大きさが同じであれば、図表による違いがあってもなくてもどちらでも良いです。今回の例では、こうなりました。

どちらの専門の学生も、オンデマンド講義を受けた後の成績が対面講義を受けた後の成績よりも5点高いというわけです。
文系では図表の有無による違いがなく、理系だと違いがある場合
次は、いよいよ交互作用がある場合です。先ほど交互作用がない場合で確認した通り、交互作用効果がないというのは、図表の有無による違いの大きさが専門分野で異ならない状態です。そうではないというためには、専門分野で図表の有無による違いの大きさが異なるか調べます。異なるといっても、色々な事なり方があります。このセクションでは、文系だと図表の有無による違いが見られないが、理系だと図表があることによって理解成績が伸びるというシナリオを示します。

グラフが示すように、文系学生は、図表に有無に関係なく理解成績は80点でした。一方、理系学生は、図表なしの文章についての理解成績は80点でしたが、図表のある文章についての理解成績は90点です。この場合、図表の有無による違いは、理系学生のみに有効だとなります。確認ですが、文系学生の場合、図表の有無による違いは0点、理系学生の場合は10点です。このように図表の有無による違いの大きさが異なる場合に、分散分析の交互作用が有意となります。
文系と理系それぞれ図表に有無による違いがあるが、効果の出方が逆な場合
授業方法による違いが、逆向きの効果で現れるような場合にも、分散分析の交互作用効果が有意となります。グラフで示すと、二つの線が交差するので、目立ちます。

ここで示されているように、文系学生の場合、図表なしだと85点、図表ありだと80点で図表がない方が理解成績が高いです。一方、理系学生の場合、図表なしだと75点、図表ありあと90点で図表があった方がよいとなります。これも、図表の有無による違いの大きさが専門分野によって異なるので交互作用は有意になります。
ここまでのまとめ
2要因分散分析における交互作用とは、ある要因の効果(今回の例では図表の有無による違い)の大きさが、他方の要因の水準次第で(例では文系か理系か)異なるかどうかを示しています。交互作用が現れるパターンを2つ示しましたが、他にも色々なパターンがあります。そして、気づいて欲しいのは、交互作用が有意になったからといって、どの条件とどの条件に差があるのかを直ちに決定できないことです。これを明らかにするために、次から説明する単純主効果検定を実施します。
単純主効果検定
単純主効果検定では、1つの要因について、ある水準だけの場合を取り上げて、そのデータの範囲内で、もう一方の要因の効果の有意性を検証します。今回の例では、文系の場合、もしくは理系の場合のデータというように、データを一旦分割して、分割されたそれぞれのデータを用いて、図表の有無による違いの検定(この例ならt検定)を行います。ここで、2回のt検定を行うので、有意水準に関する調整が必要です。調整しないと、実際には差がないのにもかかわらず、検定の中で誤って有意差ありとなってしまう可能性が高まります。調整方法はいろいろありますが、しばしば用いられるBonferroni法では、p値に検定する回数をかけて、それでも5%未満になるかを検証します。
注意:分散分析と単純主効果検定の順序
ここで注意して欲しいのは、分散分析が必ず先行します。さらに、分散分析で交互作用が有意になった場合にだけ、単純主効果検定を行うのが一般的です。(研究仮説として、どうしても細かい場合分けを見なければならない場合には、交互作用効果が有意にならなくても、単純主効果検定を実施することがあります。)
*1:この時点で訳がわからないと後半は苦しいです
多重共線性によって重回帰分析の推定は不安定になる(のはなぜか?)
今回は、回帰分析を実用する上で気をつけたい問題の1つである多重共線性について考えます。
多重共線性って?
回帰分析では、一つの従属変数(予測される変数)に対して一つ以上の独立変数(予測する変数)を構成して予測モデルとします*1。このとき、予測する変数を「独立変数」と呼ぶように、予測する変数の間には関連性がない(つまり独立)ことが想定されています。複数の変数で予測するなら似たような者同士ではなく、異なるもので予測したほうが意味があると思えるので、この想定は納得のいくものです。
しかし、社会科学領域でしばしば起こるのですが、何かの調査項目同士にはある程度相関関係が見られます。
ここで相関が少しでも高いと直ちに回帰モデルが作れないわけではなく、ある程度は独立変数間に相関があっても分析可能です。しかし、独立変数間に極端に高い相関があると、予測そのものが不安定になることがあります。例えば、独立変数について推定される回帰係数の正負が直感と反するというようなことが起きます。このような不安定な予測状況を多重共線性による問題があるという言い方をします。
定義から考える原因
推定の不安定さという問題をまずは推定式から考えてみます。2つの独立変数式による回帰モデルの推定は、次のウエブサイトを参考にしました。
http://www.ritsumei.ac.jp/se/rv/dse/jukai/MRA.html
まず、yを予測するためのx1,x2という回帰モデルを考えます。
この中のb1を推定する式は以下の通りです。証明は、参考ウエブサイトをぜひご覧ください。
この式の構成を考えてみましょう。S11とS22はx1とx2の偏差平方和(つまり変数のばらつきの大きさ)です。S1yとS2yはそれぞれx1とy、x2とyの偏差積和(つまり共変する大きさ)です。そしてS12がx1、x2の偏差積和です。
さて、ちょっとだけこの式を離れてx1とx2の相関を示す式を考えます。なぜかというと多重共線性が独立変数間の相関が高いときに生じるからです。
この式を先ほどの推定式の形式で書き換えると次のようになります。
2つの変数の相関が極端に高い場合、つまり1に近い場合は上の式の分子と分母がほぼ同じ値になることを意味します。これを利用して、
最初の式の分母を考えてみましょう。式の分母はそれぞれの変数の偏差平方和の積から二つの変数の偏差積和の2乗を引いたものです。つまり、相関係数が1に近いときには分母全体が0に近づきます。一般に分母が0に近づいていくときには分数全体の値が大きくなります。
次に分子をみてみると観測された従属変数と2つの独立変数との偏差積和が出てきます。観測された値は、母集団からのサンプルとみなされるので、観測のたびにばらつきます。先ほど考えた分母が0に近い状況を思い出すと、このばらつきの影響がより強調されると考えられます。
ここまでを要約すると、2つの独立変数間に高い相関がみられる場合には、回帰モデルにおいて推定された回帰係数のばらつきが大きくなります。推定値のばらつきの大きさは、予測の不安定さと言い換えても良いように思えます。というわけで、ここに多重共線性の不安定さが現れると考えられます。
シミュレーションで確かめる
上記のように回帰モデルの推定式から多重共線性における推定の不安定さを考えてみましたが、どうにも抽象的でわかりにくいです。そこで、実際の数値例を利用して上記の考えを確かめてみたいと思います。なお計算にはR言語を用います。
最初に平均100、標準偏差10の正規分布からランダムに1000個のデータをサンプルして従属変数とします。
DependentVar <- rnorm(1000,100,10)
さらに固有値分解という技術を使って、任意の相関係数を持つ2変数を作ります。今回は非常に高い正の相関がみられる場合としてr = 0.95のときと低い相関がみられる場合としてr = 0.1のときを考えましょう。HighCorrVarsにはr = 0.95となる2変数、LowCorrVarsにはr = 0.1となる2変数がそれぞれ含まれています。ケース数は従属変数と同じく1000です。ここで重要なことは、従属変数と独立変数の間には仮想的に無相関となるようなデータ作成法をしていることです。つまり、独立変数は従属変数に対して有意な寄与がない(つまり予測できない)はずです。
ここで交差妥当化の考え方に従って、回帰モデルの安定性を考えてみます。今、ランダムにサンプルされた1000ケースから、さらにランダムに100ケースを選んで回帰モデルのデータとしてみます。これを1000回繰り返すことで、回帰係数のばらつきを評価してみたいと思います。
#1つの独立変数の回帰係数を保存するための配列 #高い相関の場合用 HighCoefArr <- rep(NA, 1000) #低い相関の場合用 LowCoefArr <- rep(NA, 1000) for (i in 1:1000){ #選ぶケース番号をランダムに設定 randomCaseNum <- sample(1:1000, 100) #高い相関を持つ独立変数による回帰分析 resHigh <- lm(DV[randomCaseNum] ~HighCorrVars[randomCaseNum,1] + HighCorrVars[randomCaseNum,2]) #低い相関を持つ独立変数による回帰分析 resLow <- lm(DV[randomCaseNum] ~ LowCorrVars[randomCaseNum,1] + LowCorrVars[randomCaseNum,2]) #1つめの独立変数の回帰係数を保存 HighCoefArr[i] <- resHigh$coefficients[2] LowCoefArr[i] <- resLow$coefficients[2] }
このような計算をした結果、回帰係数の分布は以下のようになりました。
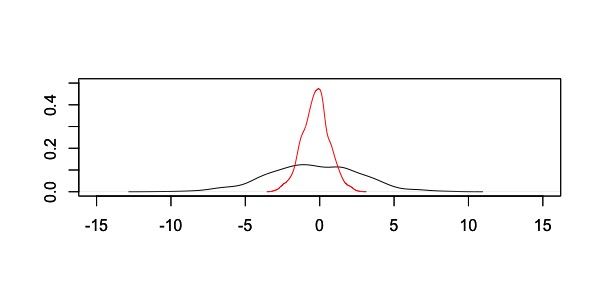
黒が高い相関がみられる独立変数で回帰分析した場合、赤い線は低い相関がみられる独立変数で回帰分析した場合です。分布から明らかなように、高い相関がみられる独立変数を用いると推定された回帰係数の取りうる範囲が広がります。つまり、極端な値が出る可能性が相対的に高く、推定が不安定であると考えられます。
まとめ
今回は、回帰分析の多重共線性の問題を数式とシミュレーションから考えてみました。その結果、多重共線性の問題が回帰係数の推定の不安定さにつながっていることを確認しました。統計学の教科書には、たいてい多重共線性の話題が取り上げられていますが、どうして推定が不安定なのかを述べられることは稀です。しかし、R言語を利用すればシミュレーションを簡単に設定してこういった問題を確認することができます。
*1:従属変数を応答変数、独立変数を予測変数と呼ぶこともあります
標準偏差と平均偏差の使い分け
本日は、割と当たり前に使っていた統計の知識でも、「なぜ」そうするのかを知らなかったという話です。統計学は、実学としての側面を持っているので、こんなことが起きるんですよね。
標準偏差と平均偏差
標準偏差と平均偏差はどちらもデータのばらつきの指標です。下の定義式を見てもらえば分かりやすいと思います。
標準偏差は、代表値からのズレを2乗したものを足し合わせて、データの個数(またはデータの個数−1)で割ったものの平方根です。
一方、平均偏差は代表値からのズレの絶対値を求めて、すべてのデータの個数(またはデータの個数−1
)で割ったものです。
平均偏差を使わないのはなぜ?
一般的にばらつきの指標は標準偏差が利用されます。平均偏差は使われるのを見たことがありません。検索サイトなどで調べると計算の便利さをとって標準偏差が用いられるとあります。確かに、絶対値は場合分けが実際の計算で場合分けが必要になるので、自乗した和の平方根を取る手続きの方が簡単です。
しかし、よく調べてみるとそれだけではないことがわかりました。以下のサイトでは、各データ要素について代表値からのずれを評価する方法として損失関数というアイデアを挙げています。実証的なデータに統計学を利用する場合、データサンプルもしくは母集団の代表値として最も妥当な値を1つ選びます。その妥当性を評価する上で、損失関数を設定する分けです。
詳しくは、ぜひリンク先を見て欲しいのですが、ここで損失関数として標準偏差のようにずれの自乗を計算するか、平均偏差のようにずれの絶対値をとるかで代表値の推定が異なることが指摘されています。ずれの自乗を計算する場合は、いわゆる最小二乗法なので、平均値が代表値となります。一方、ずれの絶対値を計算すると、最も損が少ない値はデータの中央値になるということです。
シミュレーションで確認してみる
では、簡単な数値シミュレーションをして、標準偏差と平均偏差が最も小さくなるときの代表値がそれぞれ平均値と中央値になることを確かめましょう。
検証にはR言語を使います。今回の検証では、確率分布からデータをランダムに発生させます。ここで正規分布を採用すると、平均値と中央値のずれがほとんどないと予想できるので、あえて違う確率分布(対数正規分布)を用います。
# データの生成 simData <- rlnorm(1000)
シミュレーションでは、生成したデータの最低値と最高値を計算します。最初に最低値を分布の代表値と仮定し、標準偏差と平均偏差をそれぞれ求めます。次に、最低値よりも少しだけ大きな値を代表値にします。そして、データの最大値を代表値とする場合まで、次々に繰り返します。
最後に、すべての計算結果からいつ標準偏差と平均偏差が最小になるかを調べてみましょう。
#最小値と最大値の取得 minData <- min(simData) maxData <- max(simData) #繰り返しの回数を求める numIteration<- round((maxData - minData)/0.0001) #計算結果の保存用配列を作成 ## 標準偏差用 arrSD <- NULL ## 平均偏差用 arrAD <- NULL for (i in 1:numIteration){ repData <- minData + 0.0001 * i resSD <- sqrt(sum((simData - repData)^2)/length(simData)) resAD <- sum(abs(simData - repData))/length(simData) arrSD <- c(arrSD, resSD) arrAD <- c(arrAD, resAD) }
一度手元のPCで計算してみたところ*1、minDataは0.04240865、maxDataは65.70159、numIterationは656592となりました。
標準偏差と平均偏差を保存したデータの中かからいつ値が最小になったのかを求めます。
# SDが最小となるような代表値 minData + 0.0001 * which.min(arrSD) # ADが最小となるような代表値 minData + 0.0001 * which.min(arrAD)
計算の結果、SDが最小となるような代表値は1.708909、ADが最小となるような代表値は0.9827087でした。
では、最後にこのデータの平均と中央値を計算してみます。
mean(simData) median(simData)
計算結果は、平均値が1.708862、中央値が0.9834444でした。正確な一致ではありませんが、おおよそ標準偏差が最小となるような代表値は、データの平均値であり、平均偏差が最小となるような代表値はデータの中央値であることがわかります。
*1:乱数の生成がコードに含まれています。よって計算結果は毎回異なります。