今回は、相関分析と回帰分析は何が違うのかを考えます。
相関と回帰の共通点、類似点
相関分析と回帰分析はどちらも、2つの連続量変数(数量型データ)の関係を調べるために行います。ここでの「連続量変数」とは、単に数字で表したデータという意味ではなく、条件が決められています。まず、この変数の尺度水準は間隔尺度です。例えば、1と2の間の1と2と3の間の1は等距離であるということです。また、この変数は確率分布として正規分布を仮定します。
以上のような共通点に加えて、二つの分析によって求めたいことがとても似ています。おおざっぱにいってしまえば、どちらも一方の変数の値の取り方の大小が、他方の値の取り方の大小と結びついているかを調べる分析です。
因果関係の有無が違う
次に、相関分析と回帰分析の違いを考えましょう。決定的に違うのは、因果関係の想定の有無です。相関分析では、変数間の因果関係を想定しません。どちらが原因、または結果でもよくて、相互に影響し合っているのでも構いません。
一方、回帰分析では、想定としての因果を明確にします*1。原因となる側の変数は独立変数、予測変数などと呼ばれます。これに対して結果となる側の変数は、従属変数、応答変数などと呼ばれます。回帰分析は、その予測を式のモデルで表すことができます。
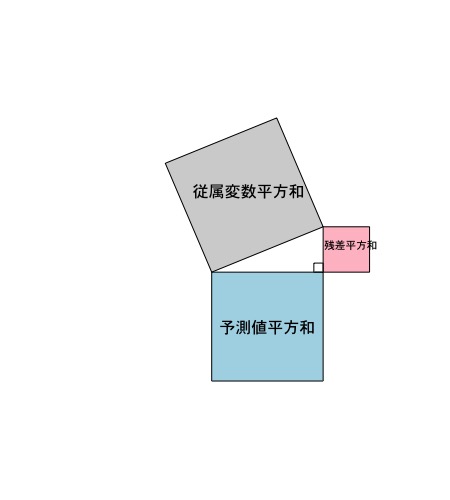
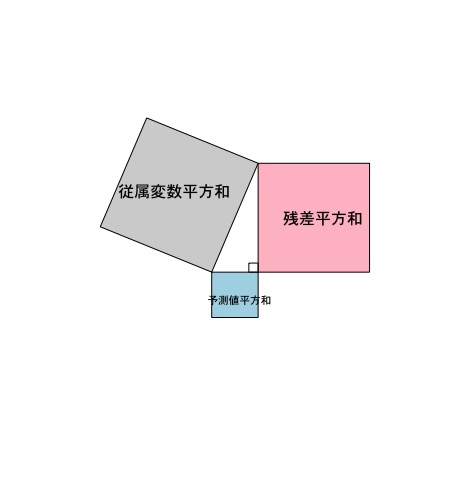
Y = a + bX + e
ここでYは従属変数(つまり予測される側)、Xは独立変数(つまり予測する側)です。aは切片、bは係数または傾き、eは残差と呼ばれています。eを除いた部分は、中学校の一次関数で出てきています。一次関数、つまり、直線を引くための式です。ここで、先ほどの切片と傾きという言葉の意味がわかると思います。切片は横軸の値(独立変数)が0のときの縦軸の値(従属変数)であり、傾きは、直線がどのような角度になるのかを表しています。回帰分析の詳細については、別の投稿でまた書きます。
R言語を利用するときの注意
相関分析では、相関係数を計算します。相関係数は-1から1までの値をとる指標で、-1に近いほど、「一方の変数の値が大きくなるほど、他方の変数の値が小さくなる」ような関係を示しています。この関係のことを負の相関関係と呼びます。また、1に近いほど「一方の変数の値が大きくなるほど、他方の変数の値も大きくなる」関係を示します。こちらは正の相関関係と呼びます。-1と1の中間、つまり0になったときは、2つの変数間に大小関係の結びつきがないことを示しています。このような場合を無相関と呼んだり、2変数が独立の関係であると言ったりします。R言語では、相関係数を求めるためにcor関数を用います。例えばvarAとvarBの相関係数を求めるなら
cor(varA,varB)
と書きます。さらに、この相関係数が0であるという帰無仮説を立てて、相関係数の有意性を検定するにはcor.test関数をつかいます。
cor.test(varA,varB)
ここで引数のとり方を逆にしても同じ値が返されます。どちらが原因とも結果とも決めていないので、強弁する強さのみが示されていると考えられます。
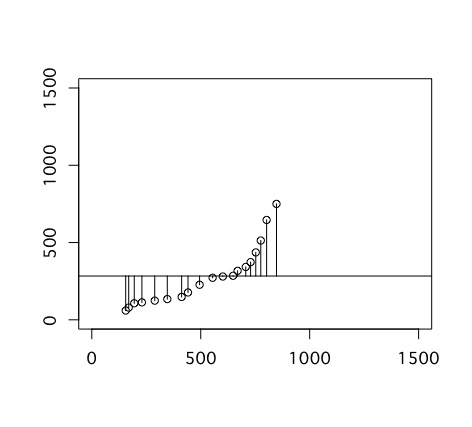
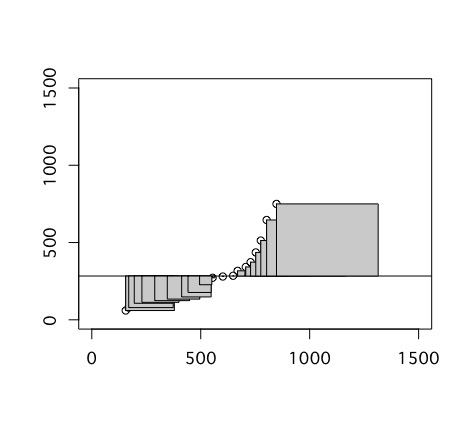
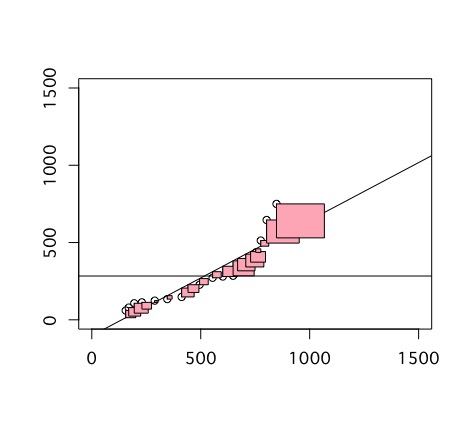
さて、2変数の関係を調べる場合、相関係数のみから結論を導くと誤った結論になることがあります。例えば、変数の中に外れ値と呼べるような極端に大きい値や小さい値が含まれていると、相関係数の絶対値は大きくなってしまいます。なので、相関関係を調べるときには、必ず散布図も書きましょう。散布図を書くにはplot関数をつかいます。
plot(varA,varB)
この例の場合、最初の引数であるvarAが横軸、2番目の引数であるvarBが縦軸の値になります。相関係数の場合と同じで、どちらを先にしても良いのですが、グラフ上のどちらの軸になっているかを覚えておきましょう。これは後で回帰分析のときに大事なポイントになります。
実際に散布図を描いてみると、正の相関が強く見られる場合では、データポイントが右肩上がりになるように分布し、負の相関関係が強く見られる場合では、データポイントの分布が右肩下がりになります。無相関の場合は、全体にまんべんなく分布します。
次に、R言語を利用して回帰分析をするには、lm関数をつかいます。
res <- lm(varB ~ varA)
summary(res)
上記の例では、resというオブジェクトに回帰分析の結果を保存しています。これをprint関数の引数として表示すると切片と傾きの推定値しか出力されません。summary関数を使うと、独立変数の傾きの有意性やモデル全体の説明率が表示されます。
また、2つの変数のうちどちらを従属変数に設定するかで、切片や傾きの推定値は異なるので注意が必要です。
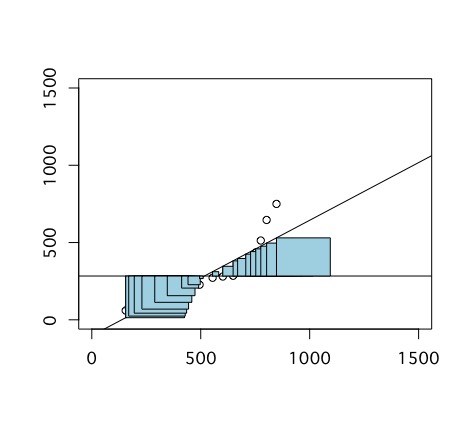
相関分析と同じように、回帰分析でも散布図が便利です。以下のようなコードで散布図に回帰直線を加えられます。
plot(varA,varB)
abline(lm(varB ~ varA))
ここで重要なのは、回帰分析ではどちらの変数を横軸、縦軸にとってもよかったのですが、回帰分析では、独立変数を横軸、従属変数を縦軸にとらなければならないことです。これを誤ると、回帰直線が散布図上のデータに全く沿わない形で描かれてしまいます。特に、plot関数では最初の引数が横軸になりますが、lm関数の式は従属変数から書き始めるので注意しましょう。
まとめ
以上をまとめると次のようになります。
- 2変数に関して、特に因果関係を想定せずに、共変動する関係にあるかどうかだけを知りたいなら相関分析(cor関数、cor.test関数)
- 2変数に関して、因果関係を想定し、一方が他方に対して持つ影響力の有無や、その予測を知りたい場合は回帰分析(lm関数)
これらを意識しながら、適切な分析方法を選ぶようにしましょう。