サンプル平均の期待値はサンプルサイズがいくつでも同じです
本日は,久々の投稿な上に,ちょっと込み入った話です。込み入っているけど,推測統計を理解するためにぜひ抑えておきたいポイントについて書きたいと思います。
サンプルの平均を母平均の推定に使う
推測統計学では,実際に持っているデータをデータを取った集団*1から持ってきた「サンプル」であるとみなします。だから,毎回毎回取ったデータが変わる可能性があります。大事なのは,今,手持ちのデータを利用して,もともとの集団全体の特徴を推定するところです。例えば,集団全体の平均(母平均)は,今持っているサンプルデータの平均として推定します*2。今あるデータから計算するしかないんだから仕方ないよね,という理解でも良いのかもしれません。でも,この方法はそんな妥協の産物というものでもなく,サンプルデータの平均値の期待値が母集団に一致することを根拠にできます*3。「サンプルデータの平均の期待値」というのが直感的ではないと思うので,これをちょっと掘り下げてみましょう*4。
数式で考える
これが平均を求める式ですね。要素数がn個のときに,そのすべての要素を足し合わせて,要素数で割れば良いです。この値の期待値を考えてみます。期待値とは,取りうる値とその確率をかけたものをすべて足し合わせたものです。
この式の分母は,要素数が決まれば定数になるので,確率を考える必要がありません。なので,E()の外に出してみましょう。
ここでE()に入っている部分は,それぞれの要素を足し合わせたものです。それがわかりやすいように書き直します。
各要素の和の期待値は,各要素の期待値の和と考えても同じことなので,式を少し変えます。
ここで,ある要素の期待値を考えてみます。ある要素の期待値は,集団の中のすべての要素が等しい確率で出ると考えると,集団全体の平均値に等しくなります。これは
でも
でも同じです。これを考えると式が以下のようになります。
平均値がn個あって,それをnで割っているので,結局はというのが,平均の期待値になるわけです。
ここで大事なポイントは,要素数nが何個であっても結局式の上で数値が変動する要素がないことです。
シミュレーションしてみる
一回一回のサンプルの値は必ずしも集団全体の平均に一致するとは限りません。でも,どんどんサンプルをとっていって,それまでのサンプルの平均をまとめて,その平均をとったらどうなるでしょうか?
まずは,10万個の全体集団を作りましょう。rnorm関数を使うと自分で決めた平均と標準偏差を持つ正規分布からランダムに値を生成してくれます。
populationData <- rnorm(100000,0,1)
今回たまたま生成した10万個のデータの平均値は0.001270158でした。では,この中から2個のデータをとってきて,サンプルを作ります。その平均値を次のように計算できます。
sampleData <- sample(populationData,2) mean(sampleData)
これを1000回ほど繰り返します。さらに,毎回,それまでの平均値のデータを利用して,「平均値の平均」を計算します。
SampleRes <- NULL Res <- NULL for ( i in 1:1000){ sampleData <- sample(populationData,2) SampleRes <- append(SampleRes, values = mean(sampleData)) Res <- append(Res, mean(SampleRes)) }
この結果を見てみましょう。まずは,サンプルを毎回取るごとの平均値はこのようになりました。
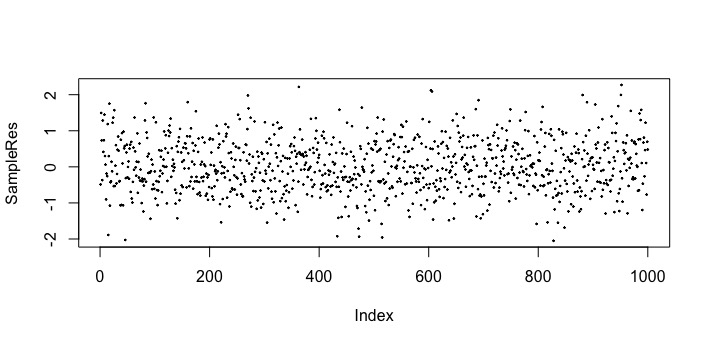
横軸は1回目から1000回めまでの回数を表していて,縦軸がサンプルの平均値です。おおよそ−2から2の範囲で値がばらついているのがわかります。さらに,毎回平均を計算するごとに平均の平均を計算したら次のようになりました。
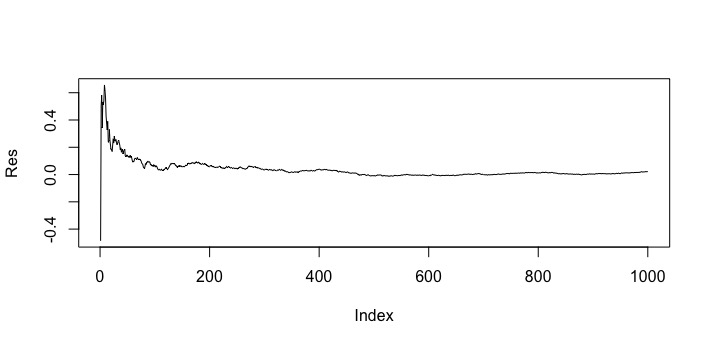
このグラフも横軸は1回目から1000回目までの回数を表しています。これを見ると,徐々に0付近に値がよっていく様子がわかります。ちなみに1000回めの平均の平均は0.0003681900でした。
では,1回のサンプルの要素数を10にしてみたらどうなるでしょうか?各回のサンプル平均は以下のようになりました。
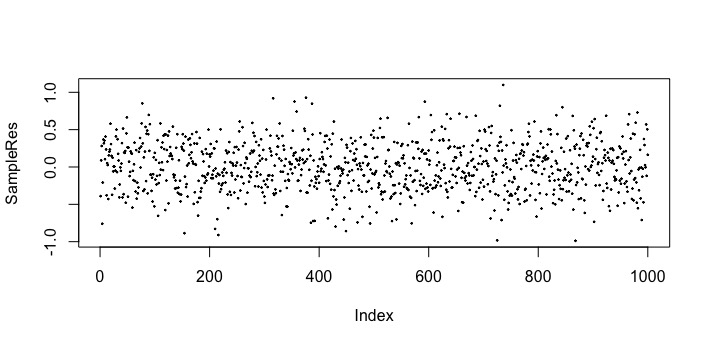
値が-1から1の間でばらついています。要素数2のときよりもばらつきが小さいように見えます。平均の平均を計算した結果は以下のようになりました。
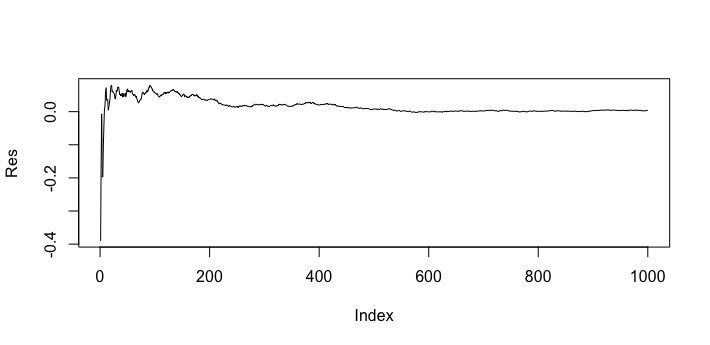
やはり計算を重ねていくと0付近に値が寄っていきます。ちなみに1000回目の「平均の平均」の値は-0.006140395でした。
このように,サンプルに含まれる要素数がいくつであろうと,もともとの集団全体の平均値に次第に近づいていくことがわかります。
まとめ
今回は,数式とシミュレーションという異なる方法を用いながら,サンプル平均の期待値が集団全体の平均になることを見てきました。