三平方の定理で理解する回帰分析における分散の分解
今回は、回帰分析の細かいモデルの話を中学校で習う「三平方の定理」を利用して考えてみます。
最小2乗法による推定
回帰分析では、最小2乗法という計算方法で、回帰直線をひくための2つの推定値(切片と傾き)を決めます。何を最小にするかというと実際に観測したデータとモデルによる推定値の間に生まれる誤差(残差と呼びます)を最小にしたいわけです。2乗というのは以下のような計算方法で残差を計算することによります。
- 予測したモデルにおける推定値と観測した値を引き算する。
- 引き算の答えを2乗する。この段階で、推定値が大きくなる場合でも、小さくなる場合でも、2乗した後の値の符号がプラスになります。
- 2乗した値を全て足しあわせます。(これを平方和と呼びます)
この計算過程は分散の計算方法によく似ています。分散では、データの各値の平均からのズレを2乗して全て足し合わせます。さらにこれをデータ数(または自由度)で割ると分散になります。この分散と残差の計算方法の類似を考慮に入れれば、データのばらつきが大きいときは残差(誤差)が大きいといえることが理解できるのではないでしょうか。
平方和の分解と分散説明率
さて、ここで回帰分析における平方和は次のように分解できます。
従属変数の平方和 = 予測された値の平方和 + 残差の平方和
そして分散説明率は以下のように評価されます。
予測された値の平方和 / 従属変数の平方和
つまり、元々ある従属変数のばらつきの何割を予測によってカバーできたかが示されています*1。ここまでの説明は、統計学のテキストで共通に出てくるのですが、わかりそうで分かりにくい表現になっている気がします。
三平方の定理の定理で理解してみよう
三平方の定理は、三角形の斜辺の二乗はその他の2辺のそれぞれの2乗和に等しいというやつです。これが上記の平方和の分解に当てはめられるのですが、それを理解するためには、まず平方和の表現を幾何学的にしてみたいと思います。
このアイデア自体は、自分で思いついたのですが、いろいろ調べてみたところ、類似の説明はすでに以下のサイトや次の書籍で行われています *2。
朝野 煕彦 (2000). 入門 多変量解析の実際 第2版 (KS理工学専門書)
http://d.hatena.ne.jp/rikunora/20131202/p1
従属変数の平方和
まず、従属変数の各サンプルの値から従属変数全体の平均を引きます。以下の図の真ん中から丸までに引かれた線分がそれです。
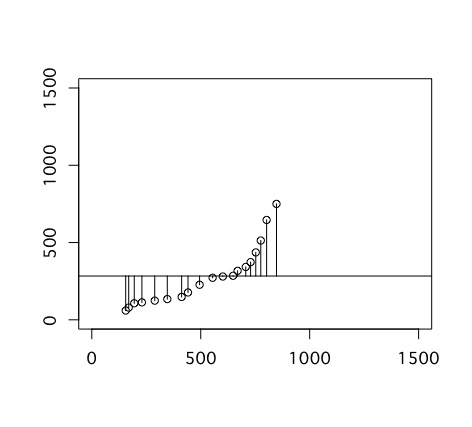
これを2乗するのですが、グラフ内では先ほどの線を一辺とする正方形の面積になります。
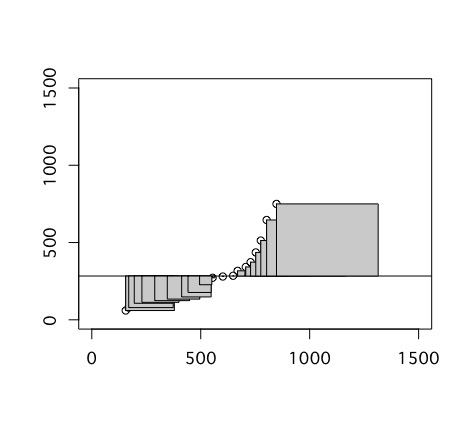
これを足し合わせたものが従属変数の平方和です。
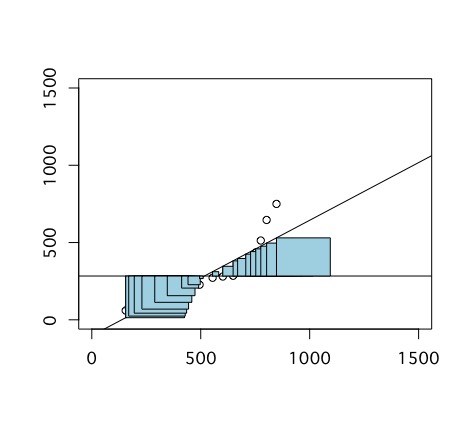
予測された値の平方和
従属変数の平方和と同じような計算方法で、予測された値の平方和を求められます。ただし、今度は、予測された値から従属変数の平均値を引いた線を一辺とする正方形を作り、それを足し合わせます。
残差の平方和
残差の平方和は、各サンプルの値から、それに対応する予測値を引きます。この線を一辺とする正方形を作り、その面積を足し合わせます。
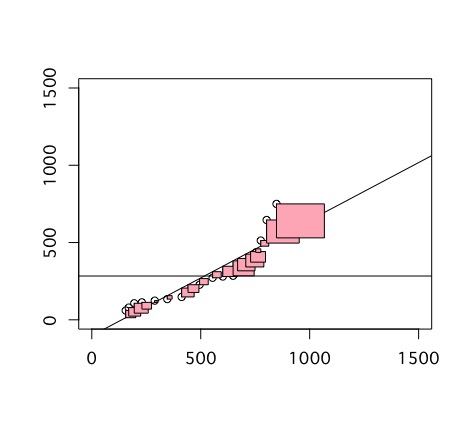
3種類の平方和を三平方の定理に当てはめる
ここまでで3種類の平方和を計算しました。これを三平方の定理に当てはめると斜辺は従属変数の平方和、残りの二辺は、予測された値の平方和と残差の平方和となります。図にすると以下のようになります。
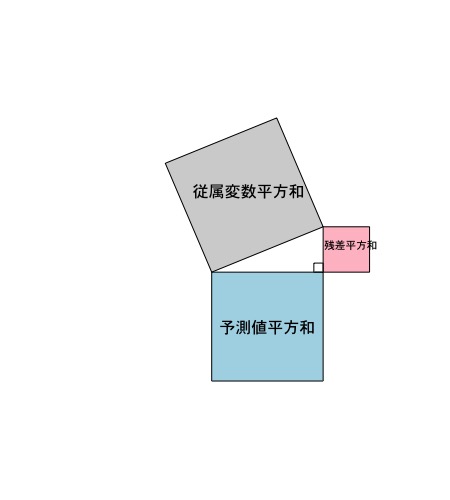
そしてこの図は、以下のような内容の理解に役立ちます。
予測値と残差の相関は0
予測値の平方和と残差の平方和は、直角になるような位置に置かれています。これは、それぞれの値が互いに影響を及ぼさない(つまり相関が0)ことを覚えるのに役立ちます。
従属変数と予測値の指す方向の類似性がモデルの説明率理解に役立つ
予測値の平方和と従属変数の平方和の位置関係は、それに対応する2辺の角度で表せます。そして、この角度は、予測値の平方和が大きくなればなるほど小さくなります。言い換えれば、2辺が指し示す方向がよく似ているということです。これは、予測値の平方和が大きいほど、モデルとしてうまく実データを説明できていることを覚えるのに役立つでしょう。
逆に、モデルとして実データがうまく説明できていないような場合は、予測値の平方和と従属変数の平方和の関係は直角に近くなります。
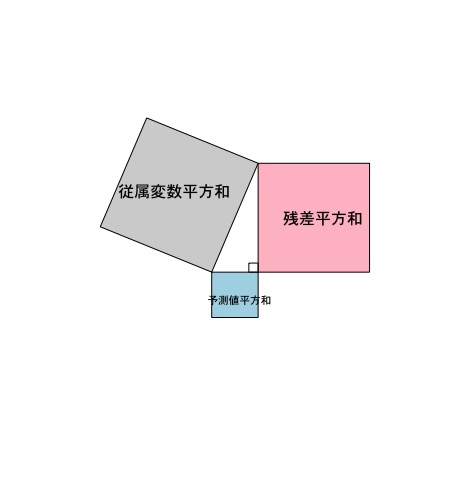
まとめ
今回は、回帰分析の各変数の散らばりを三平方の定理で考えてみました。まとめとして、回帰分析において、従属変数のデータのばらつきは、予測値のデータのばらつきと残差のばらつきに分解できることがわかりました。できるだけ予測値のデータのばらつきを大きくすることを目指して、いろいろな現象を説明、予測してみましょう。