今回は、回帰分析を実用する上で気をつけたい問題の1つである多重共線性について考えます。
多重共線性って?
回帰分析では、一つの従属変数(予測される変数)に対して一つ以上の独立変数(予測する変数)を構成して予測モデルとします*1。このとき、予測する変数を「独立変数」と呼ぶように、予測する変数の間には関連性がない(つまり独立)ことが想定されています。複数の変数で予測するなら似たような者同士ではなく、異なるもので予測したほうが意味があると思えるので、この想定は納得のいくものです。
しかし、社会科学領域でしばしば起こるのですが、何かの調査項目同士にはある程度相関関係が見られます。
ここで相関が少しでも高いと直ちに回帰モデルが作れないわけではなく、ある程度は独立変数間に相関があっても分析可能です。しかし、独立変数間に極端に高い相関があると、予測そのものが不安定になることがあります。例えば、独立変数について推定される回帰係数の正負が直感と反するというようなことが起きます。このような不安定な予測状況を多重共線性による問題があるという言い方をします。
定義から考える原因
推定の不安定さという問題をまずは推定式から考えてみます。2つの独立変数式による回帰モデルの推定は、次のウエブサイトを参考にしました。
http://www.ritsumei.ac.jp/se/rv/dse/jukai/MRA.html
まず、yを予測するためのx1,x2という回帰モデルを考えます。
この中のb1を推定する式は以下の通りです。証明は、参考ウエブサイトをぜひご覧ください。
この式の構成を考えてみましょう。S11とS22はx1とx2の偏差平方和(つまり変数のばらつきの大きさ)です。S1yとS2yはそれぞれx1とy、x2とyの偏差積和(つまり共変する大きさ)です。そしてS12がx1、x2の偏差積和です。
さて、ちょっとだけこの式を離れてx1とx2の相関を示す式を考えます。なぜかというと多重共線性が独立変数間の相関が高いときに生じるからです。
この式を先ほどの推定式の形式で書き換えると次のようになります。
2つの変数の相関が極端に高い場合、つまり1に近い場合は上の式の分子と分母がほぼ同じ値になることを意味します。これを利用して、
最初の式の分母を考えてみましょう。式の分母はそれぞれの変数の偏差平方和の積から二つの変数の偏差積和の2乗を引いたものです。つまり、相関係数が1に近いときには分母全体が0に近づきます。一般に分母が0に近づいていくときには分数全体の値が大きくなります。
次に分子をみてみると観測された従属変数と2つの独立変数との偏差積和が出てきます。観測された値は、母集団からのサンプルとみなされるので、観測のたびにばらつきます。先ほど考えた分母が0に近い状況を思い出すと、このばらつきの影響がより強調されると考えられます。
ここまでを要約すると、2つの独立変数間に高い相関がみられる場合には、回帰モデルにおいて推定された回帰係数のばらつきが大きくなります。推定値のばらつきの大きさは、予測の不安定さと言い換えても良いように思えます。というわけで、ここに多重共線性の不安定さが現れると考えられます。
シミュレーションで確かめる
上記のように回帰モデルの推定式から多重共線性における推定の不安定さを考えてみましたが、どうにも抽象的でわかりにくいです。そこで、実際の数値例を利用して上記の考えを確かめてみたいと思います。なお計算にはR言語を用います。
最初に平均100、標準偏差10の正規分布からランダムに1000個のデータをサンプルして従属変数とします。
DependentVar <- rnorm(1000,100,10)
さらに固有値分解という技術を使って、任意の相関係数を持つ2変数を作ります。今回は非常に高い正の相関がみられる場合としてr = 0.95のときと低い相関がみられる場合としてr = 0.1のときを考えましょう。HighCorrVarsにはr = 0.95となる2変数、LowCorrVarsにはr = 0.1となる2変数がそれぞれ含まれています。ケース数は従属変数と同じく1000です。ここで重要なことは、従属変数と独立変数の間には仮想的に無相関となるようなデータ作成法をしていることです。つまり、独立変数は従属変数に対して有意な寄与がない(つまり予測できない)はずです。
ここで交差妥当化の考え方に従って、回帰モデルの安定性を考えてみます。今、ランダムにサンプルされた1000ケースから、さらにランダムに100ケースを選んで回帰モデルのデータとしてみます。これを1000回繰り返すことで、回帰係数のばらつきを評価してみたいと思います。
#1つの独立変数の回帰係数を保存するための配列 #高い相関の場合用 HighCoefArr <- rep(NA, 1000) #低い相関の場合用 LowCoefArr <- rep(NA, 1000) for (i in 1:1000){ #選ぶケース番号をランダムに設定 randomCaseNum <- sample(1:1000, 100) #高い相関を持つ独立変数による回帰分析 resHigh <- lm(DV[randomCaseNum] ~HighCorrVars[randomCaseNum,1] + HighCorrVars[randomCaseNum,2]) #低い相関を持つ独立変数による回帰分析 resLow <- lm(DV[randomCaseNum] ~ LowCorrVars[randomCaseNum,1] + LowCorrVars[randomCaseNum,2]) #1つめの独立変数の回帰係数を保存 HighCoefArr[i] <- resHigh$coefficients[2] LowCoefArr[i] <- resLow$coefficients[2] }
このような計算をした結果、回帰係数の分布は以下のようになりました。
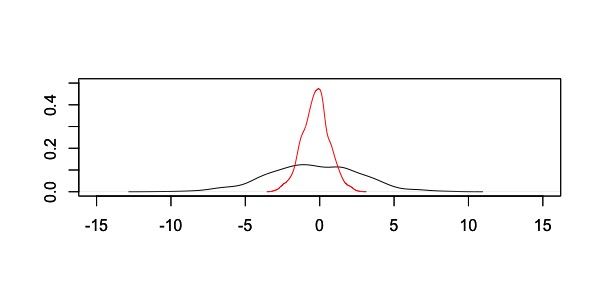
黒が高い相関がみられる独立変数で回帰分析した場合、赤い線は低い相関がみられる独立変数で回帰分析した場合です。分布から明らかなように、高い相関がみられる独立変数を用いると推定された回帰係数の取りうる範囲が広がります。つまり、極端な値が出る可能性が相対的に高く、推定が不安定であると考えられます。
まとめ
今回は、回帰分析の多重共線性の問題を数式とシミュレーションから考えてみました。その結果、多重共線性の問題が回帰係数の推定の不安定さにつながっていることを確認しました。統計学の教科書には、たいてい多重共線性の話題が取り上げられていますが、どうして推定が不安定なのかを述べられることは稀です。しかし、R言語を利用すればシミュレーションを簡単に設定してこういった問題を確認することができます。
*1:従属変数を応答変数、独立変数を予測変数と呼ぶこともあります